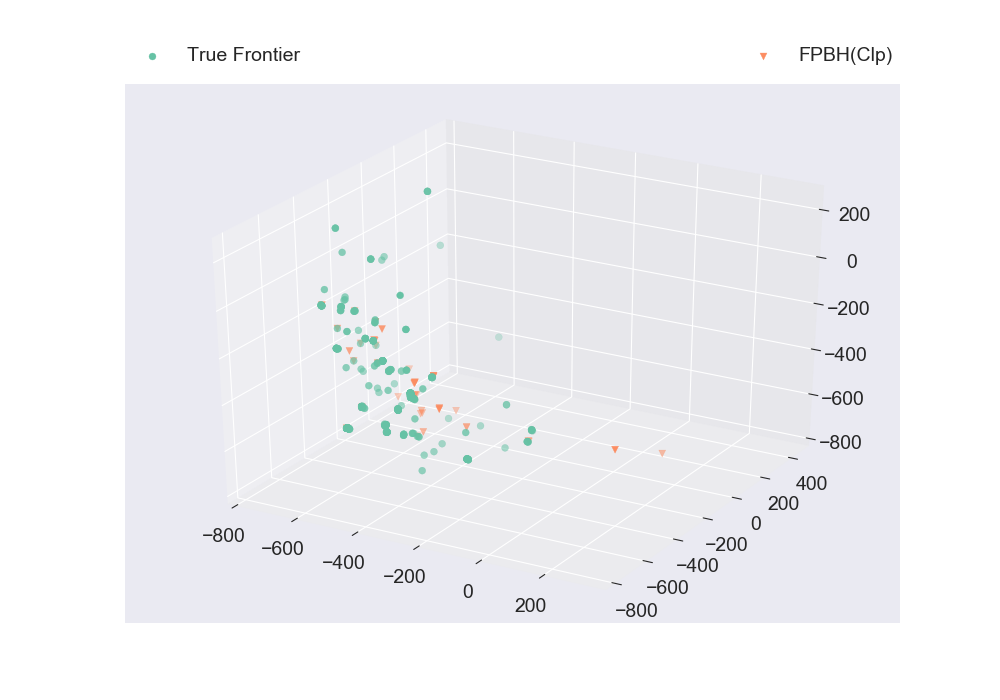
using Modolib
instance, true_frontier = read_boap_hadi(10)
@time solutions = fpbh(instance, lp_solver=ClpSolver(), timelimit=10.0)
nondominated_frontier = wrap_sols_into_array(solutions)
hg, c, mc, ac, u = compute_quality_of_apprx_frontier(nondominated_frontier, true_frontier)
println("
Hypervolume Gap = $hg %
Cardinality = $c %
Maximum Coverage = $mc
Average Coverage = $ac
Uniformity = $u")
hg, c, mc, ac, u = compute_quality_of_norm_apprx_frontier(nondominated_frontier, true_frontier)
println("
Hypervolume Gap = $hg %
Cardinality = $c %
Maximum Coverage = $mc
Average Coverage = $ac
Uniformity = $u")
plt_discrete_non_dom_frntr([true_frontier, nondominated_frontier], ["True Frontier", "FPBH(Clp)"], false, "Plot2.png")
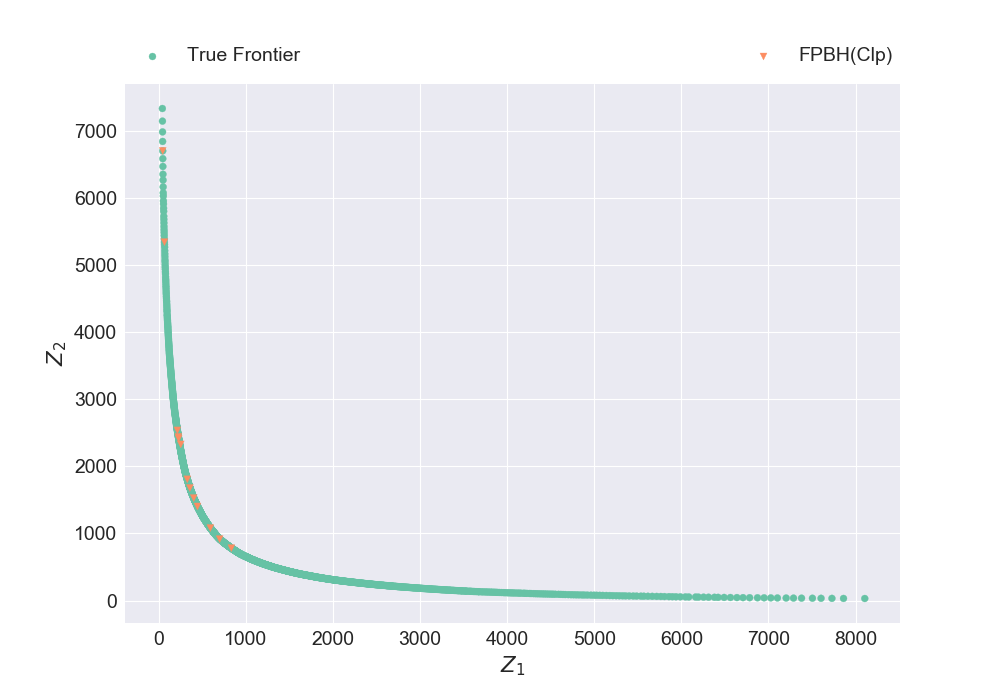
instance, true_frontier = read_bokp_xavier1("2KP150-1A")
@time solutions = fpbh(instance, lp_solver=ClpSolver(), timelimit=10.0)
nondominated_frontier = wrap_sols_into_array(solutions)
plt_discrete_non_dom_frntr([true_frontier, nondominated_frontier], ["True Frontier", "FPBH(Clp)"], false, "Plot3.png")
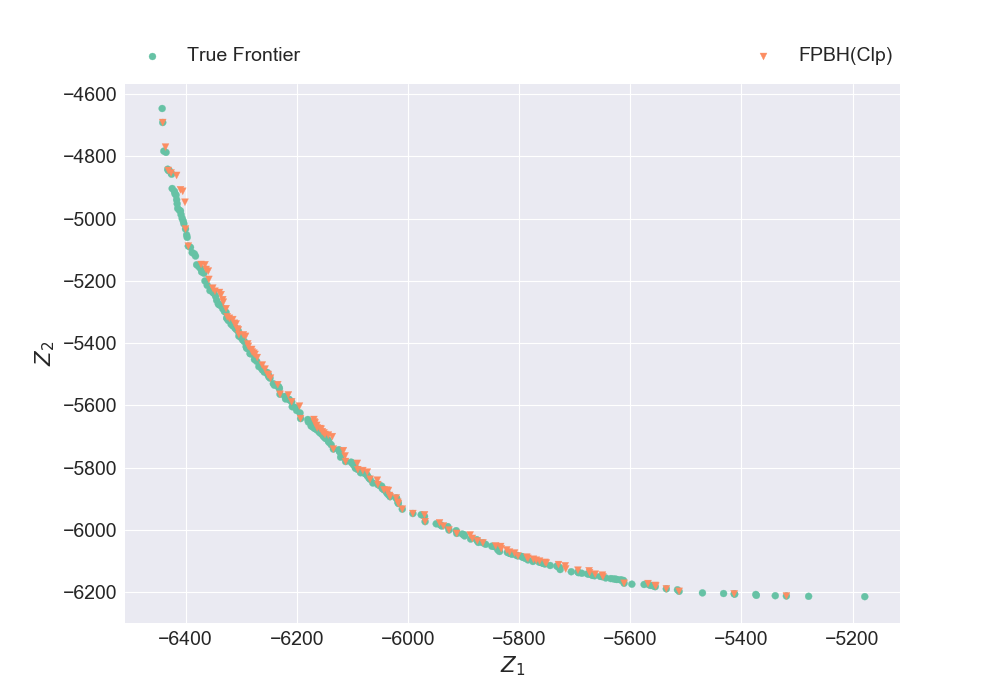
instance, true_frontier = read_bokp_hadi(1)
@time solutions = fpbh(instance, lp_solver=ClpSolver(), timelimit=10.0)
nondominated_frontier = wrap_sols_into_array(solutions)
plt_discrete_non_dom_frntr([true_frontier, nondominated_frontier], ["True Frontier", "FPBH(Clp)"], false, "Plot4.png")
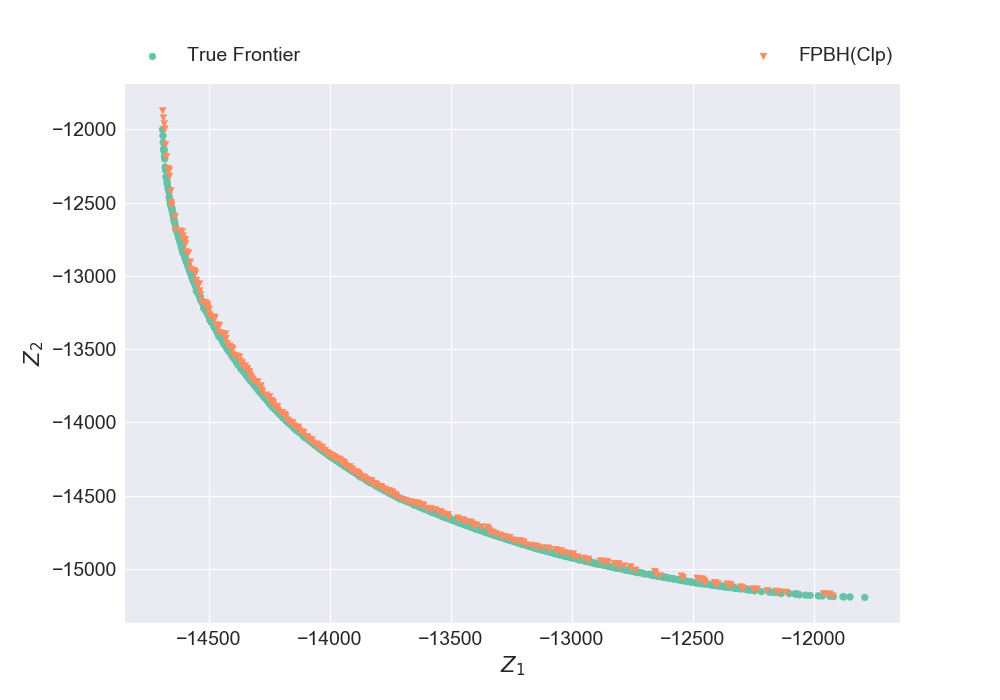
instance, true_frontier = read_boscp_xavier(100, 10, "a")
@time solutions = fpbh(instance, lp_solver=ClpSolver(), timelimit=10.0)
nondominated_frontier = wrap_sols_into_array(solutions)
plt_discrete_non_dom_frntr([true_frontier, nondominated_frontier], ["True Frontier", "FPBH(Clp)"], false, "Plot5.png")
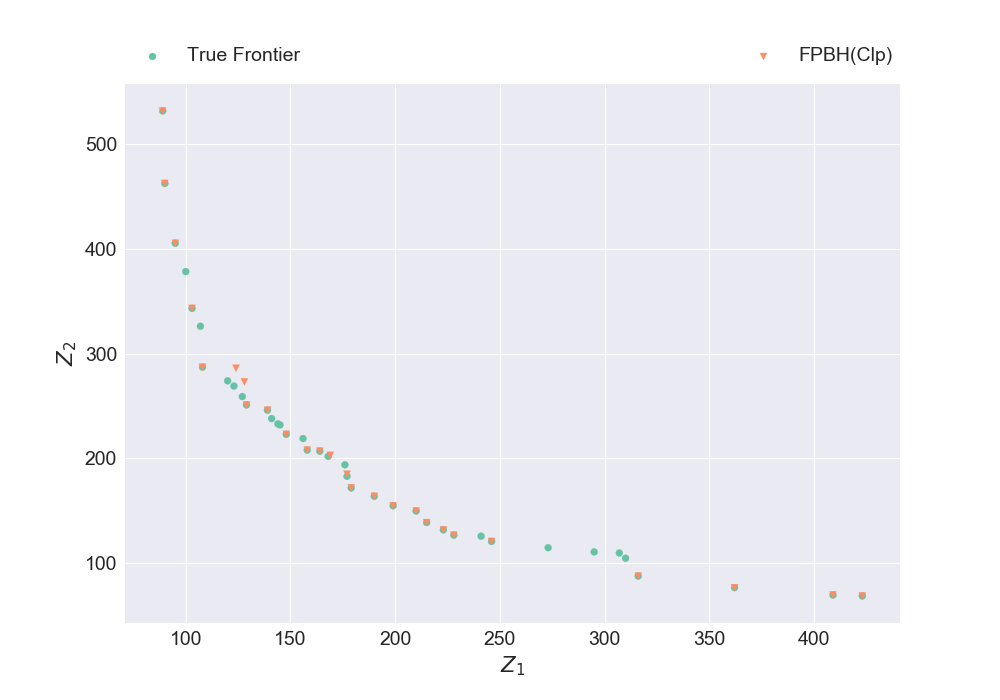
instance, true_frontier = read_bospp_xavier("2mis100_300A")
@time solutions = fpbh(instance, lp_solver=ClpSolver(), timelimit=10.0)
nondominated_frontier = wrap_sols_into_array(solutions)
plt_discrete_non_dom_frntr([true_frontier, nondominated_frontier], ["True Frontier", "FPBH(Clp)"], false, "Plot6.png")
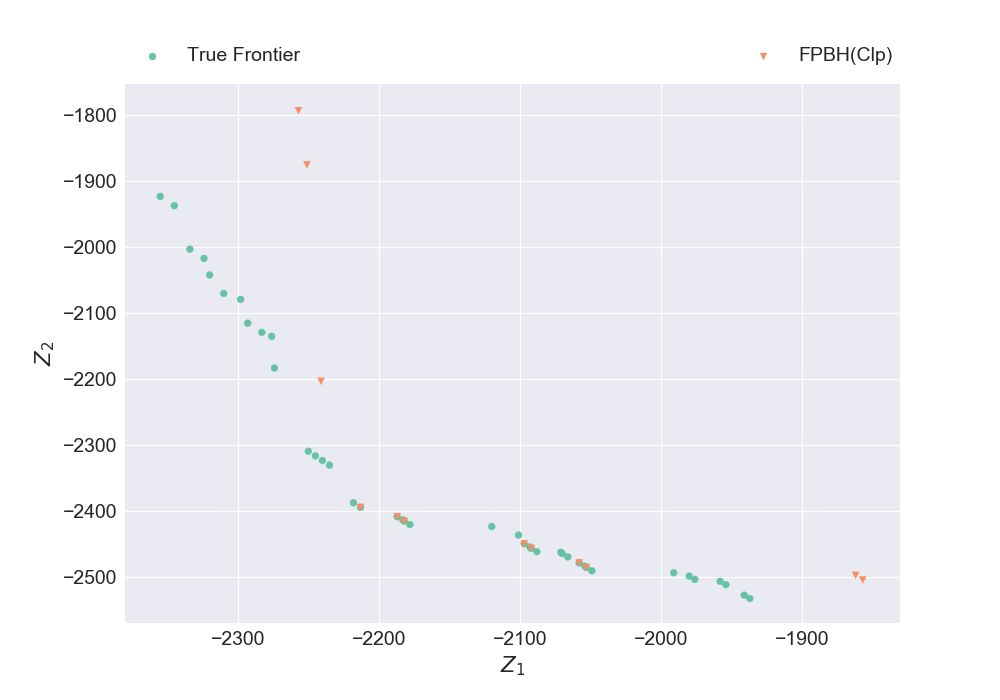
instance, true_frontier = read_bomip_hadi(6)
@time solutions = fpbh(instance, lp_solver=ClpSolver(), timelimit=10.0)
nondominated_frontier = wrap_sols_into_array(solutions)
hg, c, mc, ac, u = compute_quality_of_apprx_frontier(nondominated_frontier, true_frontier, true)
println("
Hypervolume Gap = $hg %
Cardinality = $c %
Maximum Coverage = $mc
Average Coverage = $ac
Uniformity = $u")
hg, c, mc, ac, u = compute_quality_of_norm_apprx_frontier(nondominated_frontier, true_frontier, true)
println("
Hypervolume Gap = $hg %
Cardinality = $c %
Maximum Coverage = $mc
Average Coverage = $ac
Uniformity = $u")
plt_non_dom_frntr_bomip([true_frontier, nondominated_frontier], ["True Frontier", "FPBH(Clp)"], "Plot7.png")
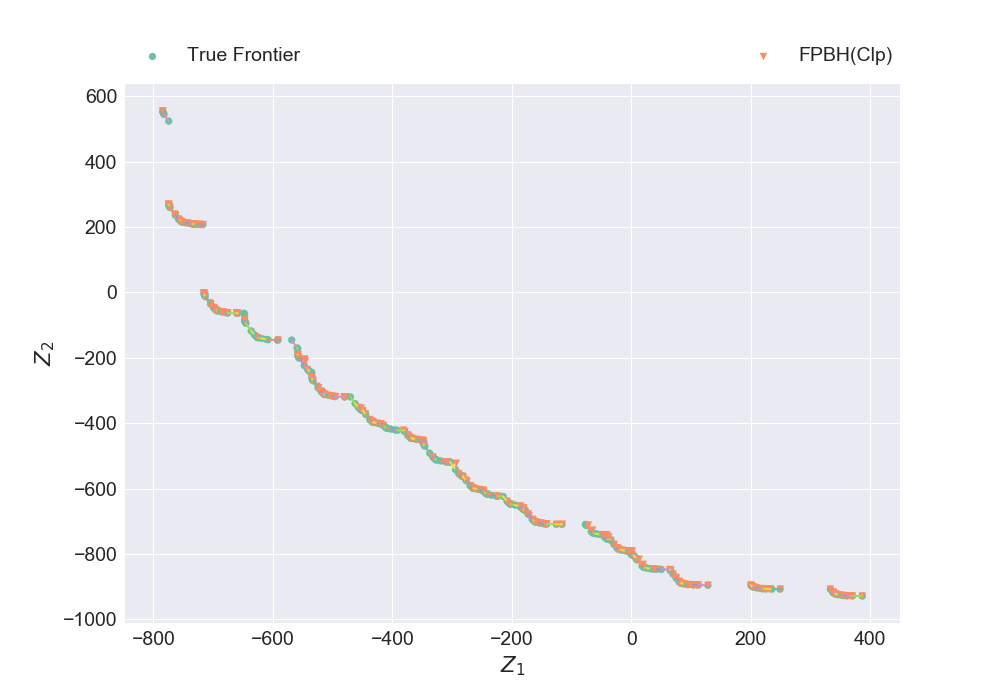
instance, true_frontier = read_bouflp_hadi(12)
@time solutions = fpbh(instance, lp_solver=ClpSolver(), timelimit=10.0)
nondominated_frontier = wrap_sols_into_array(solutions)
plt_non_dom_frntr_bomip([true_frontier, nondominated_frontier], ["True Frontier", "FPBH(Clp)"], "Plot8.png")
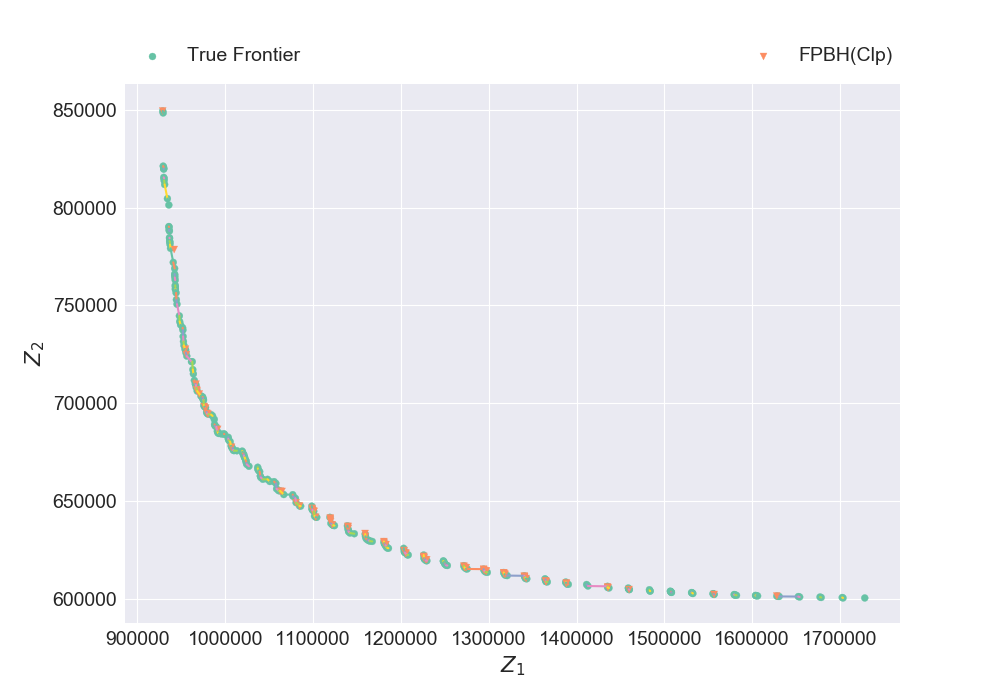
instance, true_frontier = read_moap_kirlik(3, 5, 1)
@time solutions = fpbh(instance, lp_solver=ClpSolver(), timelimit=10.0)
nondominated_frontier = wrap_sols_into_array(solutions)
hg, c, mc, ac, u = compute_quality_of_apprx_frontier(nondominated_frontier, true_frontier)
println("
Hypervolume Gap = $hg %
Cardinality = $c %
Maximum Coverage = $mc
Average Coverage = $ac
Uniformity = $u")
hg, c, mc, ac, u = compute_quality_of_norm_apprx_frontier(nondominated_frontier, true_frontier)
println("
Hypervolume Gap = $hg %
Cardinality = $c %
Maximum Coverage = $mc
Average Coverage = $ac
Uniformity = $u")
plt_discrete_non_dom_frntr([true_frontier, nondominated_frontier], ["True Frontier", "FPBH(Clp)"], false, "Plot9.png")
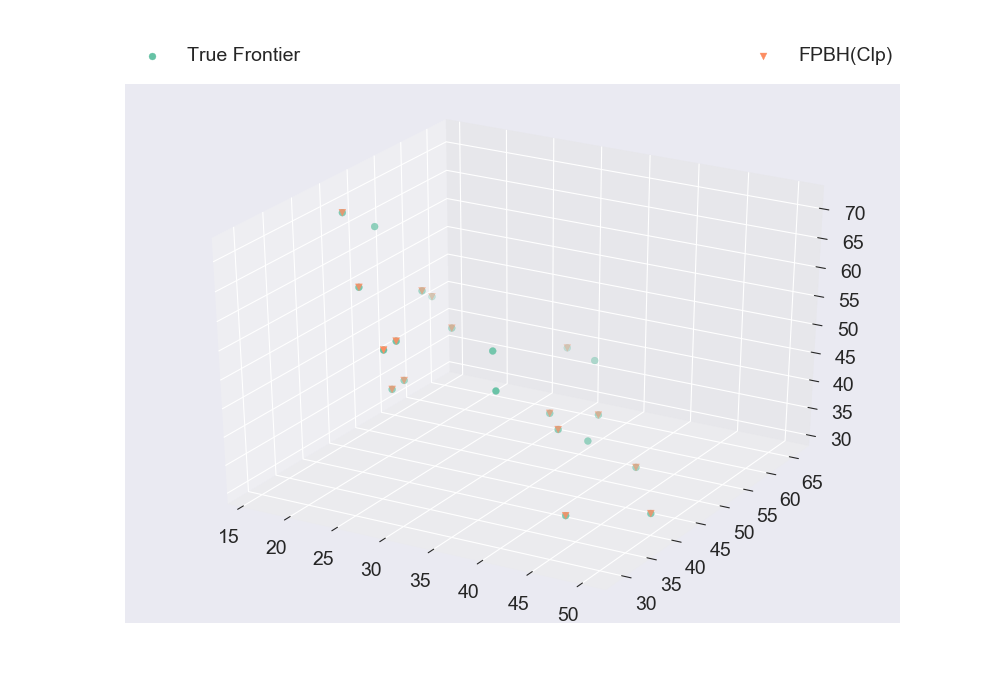
instance, true_frontier = read_mokp_kirlik(3, 10, 1)
@time solutions = fpbh(instance, lp_solver=ClpSolver(), timelimit=10.0)
nondominated_frontier = wrap_sols_into_array(solutions)
plt_discrete_non_dom_frntr([true_frontier, nondominated_frontier], ["True Frontier", "FPBH(Clp)"], false, "Plot10.png")
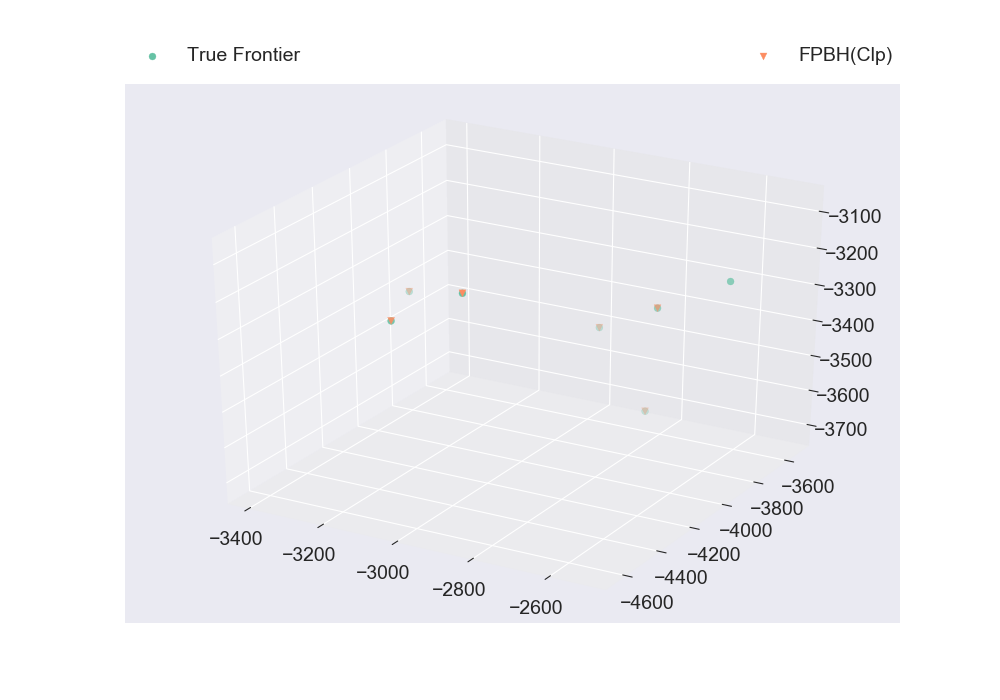
instance, true_frontier = read_mombp_aritra(3, 320, 1)
@time solutions = fpbh(instance, lp_solver=ClpSolver(), timelimit=10.0)
nondominated_frontier = wrap_sols_into_array(solutions)
plt_discrete_non_dom_frntr([true_frontier, nondominated_frontier], ["True Frontier", "FPBH(Clp)"], false, "Plot11.png")